LENTES
Una lente es un sistema óptico
centrado formado por dos dioptrios de los cuales uno, por lo menos, acostumbra
a ser esférico. Las lentes pueden
ser negativas o positivas y ambas son utilizadas en la construcción de los
objetivos.
Lente Convexa:
· Lente positiva
· Más gruesa en el centro que en los bordes.
· Se llama positiva porque desvía los rayos de luz hacia
su foco y por tanto puede proyectar imágenes sobre una superficie plana.
· Mirando a través de ella, tenemos que moverla para
poder enfocar y en algún momento se nos invertirá la imagen que vemos
· Es la lente necesaria para la creación de un objetivo
Lente cóncava
·
Lente negativa
· Desvía los rayos de luz, con lo que se impide la formación
de una imagen sobre una superficie plana
· Produce imágenes claras para el ojo mirando a través
de ella, es decir enfocadas, y la imagen no quedara invertida,
independientemente de la distancia a la que está el sujeto
LENTES DELGADAS.
Una lente delgada es una abstracción
de una lente. En su caso más sencillo es una lente de vidrio formada por la
intersección de dos esferas de igual radio, pero con la particularidad de que
su espesor es mucho más pequeño que el radio de las esferas.
Definiciones:
a) Eje de la lente (o eje óptico) es una
línea imaginaria que conecta los centros de las dos esferas. (línea que une C1
y C2 en la figura).
b) Centro óptico es el centro geométrico de
la lente. Se encuentra sobre el eje óptico (O en la figura).
Una lente delgada (convergente) se representa de forma simplificada tal como aparece en la figura
Una lente delgada (convergente) se representa de forma simplificada tal como aparece en la figura
c) La longitud focal de una lente delgada
puede definirse como:
c.1) La
distancia entre un punto denominado Foco objeto y el Centro óptico, cuya imagen
se encuentra en el infinito. (F1 en la figura)
c.2) La
distancia entre un punto denominado Foco imagen y el Centro óptico, que es la
imagen de un punto situado en el infinito en la escena. (F2 en la figura)
Circunstancias:
1) Todo rayo paralelo al eje
óptico que proviene de la escena, pasa por el foco imagen
2) Todo rayo que pasa por el foco
objeto emerge paralelo al eje óptico.
Es posible utilizar esta información
para obtener la imagen de un objeto, PQ en la figura, por métodos puramente
gráficos. Así podemos observar en la figura que el rayo que sale de Q paralelo
al eje óptico, acaba pasando por F2.
De igual manera, el rayo que emerge
de Q y pasa por F1, sale paralelo al eje óptico. Con dos rayos únicamente ya es
posible ver cuál será el punto en que interceptan y ahí estará la imagen de P´-Q'.
Cada plano de la escena se convierte en
un plano en la imagen
EL CIRCULO DE CONFUSION.
El círculo de confusión es un valor estadístico. Es
decir, una persona, como promedio, colocada a una distancia de alrededor de 40 cms de una fotografía de 20 x 30 cms, ve como un punto (sin
dimensiones) cualquier círculo menor de 0.25
mm. Esto significa que cualquier círculo en una fotografía con un tamaño
inferior a 0,25 mm se verá con nitidez absoluta, sin ninguna sensación de
borrosidad.
1.-Relacion de este círculo, con los
diferentes los diferentes planos focales y sus tamaños.
Camara analógica con película de 35 mm
De la película de 36mmx24 mm, a la foto de 300mm x 200mm
hay una ampliación de 8,33 (300/36=8,33). Por tanto, cualquier círculo en el
negativo con un tamaño igual o inferior a 0,25mm/8.33= 0,03 mm, se verá nítido.
Por tanto el círculo de confusión en una cámara réflex
analógica es de 0.03 mm. Pero recordemos que éste número sólo tiene sentido, si
lo relacionamos con su traslado a una imagen editada de 20 x 30 cm y observándola
a una distancia de alrededor de 40 cm.
Camara réflex digital de formato completo (sensor de 36mm x 24 mm)
Sería igual que el caso anterior
Camara con sensor APS-C
Utilizado por las réflex digitales no profesionales,
el círculo de confusión sería distinto pues la ampliación es mayor. El formato APS-C
es alrededor de 24 x 16 mm.
Realizando los mismos cálculos que en el caso
anterior, nos encontramos con que 300/24 = 12.5. Por tanto si hacemos la
división 0,25mm/12.5 = 0.02mm que es el valor del círculo de confusión para los
sensores de formato APS-C.
2.- Relación de este círculo con la resolución del
sensor:
¿Tiene alguna influencia la propia resolución del
sensor? ¿Dará lo mismo que sea de 2000 x 3000 pixeles (aproximadamente 6
megapixeles), a que sea de 4000 x 6000 (aproximadamente 24 megapixeles)?
Tratemos el caso de menor resolución. Cada pixel, en
formato FF, ocupa una longitud de (36mm/3000) en una dimensión y (24mm/2000) en
la otra. Es decir 0,012 mm en ambas dimensiones. Esta cantidad es menor de 0.03
mm. Si el sensor fuera de mayor resolución la longitud del pixel en ambas
dimensiones sería aún menor. En cualquiera de los casos lo que ocurriría sería
que el círculo de confusión estaría formado por varios pixeles en la imagen.
¿Por qué vamos a encontrar en la imagen del sensor círculos con un tamaño
superior al círculo de confusión y que nos proporcionen sensación de
borrosidad?:
La respuesta está
en el hecho de que una imagen es una visión bidimensional de algo
inherentemente tridimensional en la realidad.
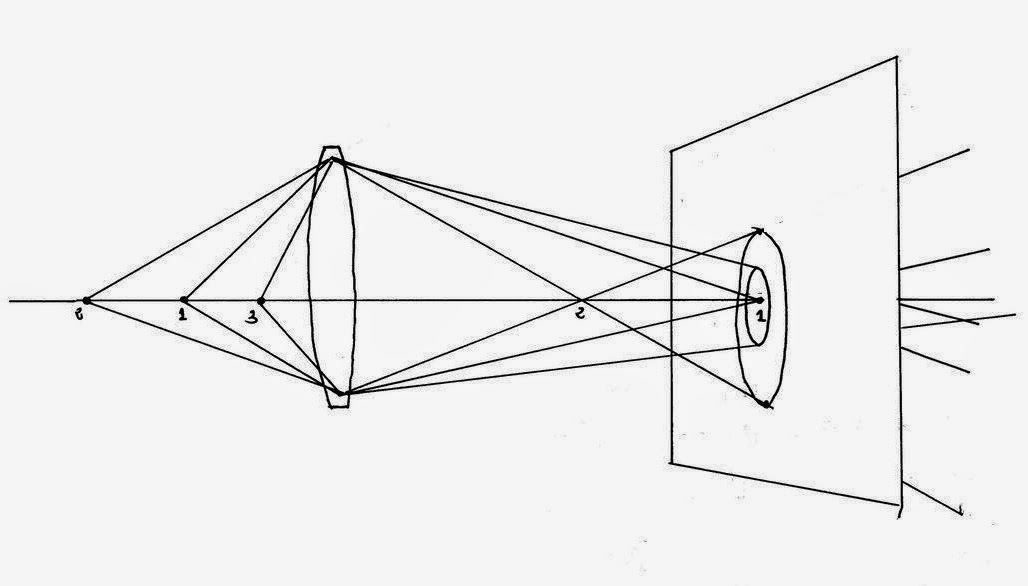
Solamente los puntos de un plano (plano que está
enfocado) de la escena convergen, por acción del objetivo, en puntos en la
imagen focal (punto 1 de la imagen)
Aquellos que se encuentran más alejados, de ese plano
concreto, convergen más cerca del objetivo (punto 2, que converge en 2').
Los más próximos al objetivo (punto 3, que converge
por detrás del plano focal.)
Cuanto más nos alejemos, en la escena, del plano de
enfoque (punto 1 de la figura), los puntos formarán círculos más grandes en el
plano focal, hasta llegar a un momento en que traspasen el tamaño de 0.03 mm si
usamos una réflex FF, o bien 0.02 mm si usamos una réflex APS-C.
En ese momento se formará un círculo en la imagen del
plano focal, que al ampliarlo e imprimirlo en 20 x 30 y observarlo a 40 cms,
nos empezara a proporcionar sensación de borrosidad.
A mas alejamiento mayor borrosidad.
El concepto de círculo de confusión es la base de la comprensión de los
conceptos de profundidad de campo y
profundidad de foco
PROFUNDIDAD DE CAMPO Y PROFUNDIDAD DE FOCO
El objetivo de una cámara fotográfica está formado por varias lentes pero, para
la explicación, vamos a considerar que utilizamos una única lente convergente
equivalente al conjunto. Esta lente, que llamaremos plano del objetivo, presenta
un plano de simetría perpendicular al eje óptico (línea imaginaria que desde la
escena, atraviesa el objetivo, posteriormente el sensor, y luego continúa
indefinidamente).
Todos los puntos de cada plano de
una escena convergen en puntos que se encuentran contenidos en su
correspondiente plano imagen. Cuando
utilizamos el anillo de enfoque, lo que estamos haciendo es variar la distancia
entre el plano en el que se encuentra el sensor (plano focal) y el plano del objetivo.
Recordemos el concepto de distancia focal de un objetivo: distancia
del plano del objetivo al plano focal, que está situado sobre la longitud
focal, únicamente cuando enfocamos a infinito, lo que sería enfocar el plano de
imagen más alejado de la cámara.
Pero vamos a seleccionar otro de los
planos de la escena de tal manera que su plano imagen se constituya en el plano
focal . A este plano imagen, lo denominaremos plano de enfoque.
La profundidad de campo
Conjunto de
planos anteriores y posteriores al plano de enfoque que forman en el plano
focal círculos inferiores en tamaño al círculo de confusión.
Debido a la
limitación en la visión humana, los observamos en la imagen como perfectamente
nítidos, aún cuando en realidad, perfectamente nítido sólo hay uno: el plano de enfoque.
La profundidad de
campo hace referencia a los planos de la escena, en concreto a aquellos que
apreciamos con nitidez.
La profundidad de foco
Mide la mayor o
menor dificultad para realizar el enfoque.
Para poder
entender el concepto debemos recurrir a un experimento imaginario, tal como se
observa en la figura superior. Si movemos (hacia adelante o hacia atrás) el
plano focal, manteniendo constante el plano de enfoque, observamos que el punto
imagen 2 y se convierten en un círculo. Cuando sobrepasemos el tamaño del círculo
de confusión empezaremos a ver la imagen borrosa. Si hay poca profundidad de
foco, significa que rápidamente empezaremos a ver borroso, por tanto nos será
más sencillo enfocar. Si la profundidad de foco es mayor, tardaremos más en
observar el desenfoque y nos costará más enfocar.
Es decir que, en
este caso, cuanto peor, mejor.
Por tanto la
profundidad de foco hace referencia al desplazamiento del plano focal
necesario para que podamos apreciar la falta de nitidez.
La profundidad de
foco mide la mayor o menor dificultad para realizar el enfoque.
Es importante
comprender que lo anterior es un experimento imaginario. Si cambiamos realmente
la distancia entre el plano focal y el plano del objetivo utilizando el anillo
de enfoque, lo que conseguiremos será obtener un plano de enfoque distinto. Y
en la premisa de nuestro experimento se consideraba que el plano de enfoque
permanecía constante.
PROFUNDIDAD DE FOCO Y APERTURA DE DIAFRAGMA
Para poder entender la variación de la Profundidad de Foco en función de la Apertura del Diafragma, basta con observar las imágenes siguientes.
Observamos que la Profundidad de Foco tiene una cierta longitud delimitada por los planos en los que la intersección del ángulo sólido que pasa por el punto imagen P' forma un círculo con las dimensiones del Círculo de Confusión.
Diafragma cerrado (número f grande)


observamos que la delimitación del ángulo sólido que pasa por el punto imagen P' con los planos correspondientes en un tamaño correspondiente igualmente al Círculo de Confusión hace que éstos se abran, aumentando la Profundidad de Foco.
Por tanto se establece la siguiente regla:
a) Si la Apertura de Diafragma disminuye, aumenta la Profundidad de Foco.
b) Si la Apertura de Diafragma aumenta, disminuye la Profundidad de Foco.
PROFUNDIDAD DE FOCO Y DISTANCIA FOCAL
Para poder entender la variación de la Profundidad de Foco en función de la Longitud Focal , debemos partir de la Ecuación de Gauss correspondiente a una lente delgada.
1 1 1 1 1 1
--- + --- = --- o bien: --- = --- - ---
S S' F' S' F S
En la imagen nos
encontramos con una cierta situación de partida donde el punto objeto P, a una
distancia S del objetivo, produce el punto imagen P' a una distancia S' del
mismo.
Y una determinada
Profundidad de Foco.
Si analizamos
adecuadamente la Ecuación de Gauss, podremos seguir la siguiente cadena de
razonamientos en referencia a la figura de la parte inferior:
a) Si aumentamos la longitud focal , entonces el
valor de F´ en la figura de abajo será mayor que el valor de F'
en la figura de arriba. Por tanto la expresión 1/F' será menor en la figura de
abajo que en la de arriba.
b) El valor de S no varía pues la distancia de
enfoque no cambia. Por tanto 1/S es constante en ambas figuras.
c) La única conclusión lógica es que el valor 1/S'
debe disminuir. Y, por necesidad, S' debe aumentar. Al aumentar S' en la figura de abajo con respecto a la de arriba, el ángulo a2
será menor que el ángulo a1. (La apertura de diafragma es constante.
d) Dado que el círculo de confusión es también
constante, aumenta la Profundidad de Foco.
La ecuación de una lente delgada puede expresarse como
S´ = S* F´/(S- F´).
A partir del conocimiento de estos hechos,
calcularemos el valor de S´ para dos supuestos distintos concretos con dos
distancias (100 metros y 10 metros)
Longitud focal de 35 mm
S´1 = (100000 mm x 35) / (100000 - 35) = 35.01
S´2 = (10000 mm x 35) / (10000 - 35) = 35.12
Longitud focal de 200 mm
S´3 = (100000 x 200) / (100000 - 200) = 200.40
S´4 = (10000 x. 200) / (10000 - 200) = 204.08
Para el primer caso, todos los planos de enfoque situados
entre 100 y 10 m dan lugar a planos de imagen muy concentrados en un intervalo
de 35.12 - 35.01 = 0.11 mm.
Para el segundo caso, los mismos planos de enfoque
ubican sus planos imagen en un intervalo de 204.08 - 200.40 = 3.68 mm. Es
decir, si la longitud focal es pequeña (35mm) los planos imagen están mucho más
concentrados que si la longitud focal es grande (200mm).
Por tanto se puede
establecer la siguiente Regla:
1.
Si la Longitud Focal aumenta, aumenta
la Profundidad de Foco.
2.
Si la Longitud Focal disminuye, disminuye
la Profundidad de Foco.
Esto viene a
confirmar el hecho de que cuando utilizamos teleobjetivos de gran longitud
focal, el proceso de enfocar se vuelve más complicado.







Notable gracias publicare parte de tu contenido en una entrada de mi blog, obviamente se dara la cita de fuente respectiva.
ResponderEliminar